问题
解答题
已知二次函数y=ax2+bx+c,……(*)
(1)当a=1,b=-2,c=1时,请在图的直角坐标系中画出此时二次函数的图象;
(2)用配方法求该二次函数(*)的图象的顶点坐标。
答案
解:(1)当a=1,b=-2,c=1时,
y=x2-2x+1=(x-1)2,
所以该二次函数图象的顶点坐标为(1,0),对称轴为直线x=1,
利用函数对称性列表如下:
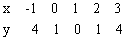
在给定的坐标系中描点,画出图象如下:
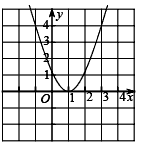 ;
;
(2)由y=ax2+bx+c是二次函数,知a≠0,
y=a(x2+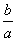 x)+c=a[x2+
x)+c=a[x2+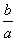 x+(
x+(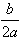 )2]+c-a×(
)2]+c-a×(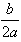 )2
)2
=a(x+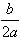 )2+
)2+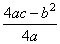 ,
,
所以该二次函数图象的顶点坐标为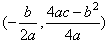 。
。
