问题
解答题
已知向量a=(-2,1),b=(x,y),
(Ⅰ)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足a·b=-1的概率;
(Ⅱ)若x,y在连续区间[1,6]上取值,求满足a·b<0的概率。
答案
解:(Ⅰ)将一枚质地均匀的正方体骰子先后抛掷两次,所包含的基本事件总数为6×6=36个;
由a·b=-1有-2x+y=-1,
所以满足a·b=-1的基本事件为(1,1),(2,3),(3,5),共3个;
故满足a·b=-1的概率为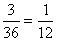 ;
;
(Ⅱ)若x,y在连续区间[1,6]上取值,则全部基本事件的结果为Ω={(x,y)|1≤x≤6,1≤y≤6};
满足a·b<0的基本事件的结果为A={(x,y)|1≤x≤6,1≤y≤6且-2x+y<0};
画出图形如下图,
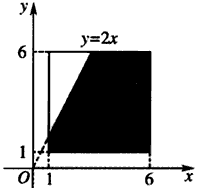
矩形的面积为S矩形=25,
阴影部分的面积为S阴影=25-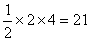 ,
,
故满足a·b<0的概率为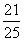 。
。
