问题
解答题
口袋里有分别标有数字1、2、3、4的4只白球和分别标有数字5、6的2只红球，这些球除了颜色和所标数字外完全相同。某人从中随机取出一球，记下球上所标数字后放回，再随机取出一球并记下球上所标数字，
（Ⅰ）求两次取出的球上的数字之和大于8的概率；
（Ⅱ）求两次取出的球颜色不同的概率。
答案
解：由题意，从口袋里任意取一球，放回后再随机取出一球，共有36个基本事件，且它们等可能发生，
（Ⅰ）设：“两次取出的球上的数字之和大于8”为事件A，
则事件A中包含两次取出的球上的号码为（3，6），（4，5），（4，6），（5，4），（5，5，），（5，6），（6，3），（6，4），（6，5），（6，6）共10个基本事件，
∴
；
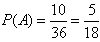（Ⅱ）设：“两次取出的球颜色不同”为事件B，
则事件B包含两次取出的球上的号码为（1，5，），（1，6），（2，5），（2，6），（3，5），（3，6），（4，5），（4，6），（5，1），（5，2），（5，3），（5，4），（6，1），（6，2），（6，3），（6，4）共16个基本事件，
∴
；
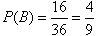答：两次取出的球上的数字之和大于8的概率是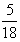
，两次取出的球颜色不同的概率是
。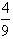