问题
解答题
某工厂要制造A种电子装置45台,B电子装置55台,为了给每台装配一个外壳,要从两种不同的薄钢板上截取,已知甲种薄钢板每张面积为2平方米,可作A的外壳3个和B的外壳5个;乙种薄钢板每张面积3平方米,可作A和B的外壳各6个,设用这两种薄钢板分别为x,y张,
(1)写出x,y满足的约束条件;
(2)x,y分别取什么值时,才能使总的用料面积最小,最小面积为多少?
答案
(1)设用甲种薄金属板x张,乙种薄金属板y张,总的用料面积为z平方米.
则可做A种的外壳为3x+5y个,B种的外壳为5x+6y个,
由题意得:
,3x+5y≥45 5x+6y≥55 x,y∈N
(2)由(1)可知
,3x+5y≥45 5x+6y≥55 x,y∈N
所有薄金属板的总面积为:z=2x+3y
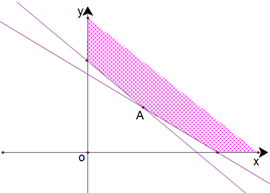
甲、乙两种薄钢板张数的取值范围如图中阴影部分所示(x,y取整数).
要使z最小,目标函数表示的直线过点A(
,5 7
),由于其不是整数点,60 7
故平移过点A的直线:z=2x+3y,当其经过平面区域内的点(2,8)时,
这时面积为28平方米,此时直线同时也经过点(5,6).
因此用甲、乙两种薄钢板的张数分别为2张、8张或者5张、6张,才能使总的用料面积最小.