问题
选择题
已知α,β是方程x2+ax+2b=0的两根,且α∈[0,1],β∈[1,2],a∈R,b∈R,求
|
答案
设f(x)=x2+ax+2b,
∵α∈[0,1],β∈[1,2],
则
,f(0)=2b≥0 f(1)=1+a+2b≤0 f(2)=4+2a+2b≥0 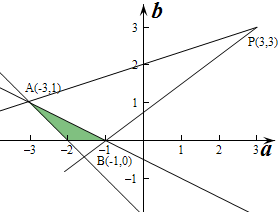
作出不等式组对应的平面区域如图:
的几何意义为点M(a,b)到定点P(3,3)连线斜率的取值范围.b-3 a-3
由图象可知直线PA的斜率最小,为
=1-3 -3-3
=-2 -6
,1 3
PB的斜率最大,为
=0-3 -1-3
.3 4
∴
的最大值与最小值之和为b-3 a-3
+1 3
=3 4
,13 12
故选:A.
