问题
解答题
已知抛物线y=x2+ax+a-2。
(1)证明:此抛物线与x轴总有两个不同的交点;
(2)a取何值时,两点间的距离最小?
答案
解:(1)∵y=x2+ax+a-2,
∴△=a2-4(a-2)=a2-4a+8=a2-4a+4+4=(a-2)2+4,
又∵(a-2)2+4>0,
∴△>0,
∴此抛物线与x轴总有两个不同的交点;
(2)设二次函数y=x2+ax+a-2与x轴的两交点的横坐标为x1,x2,
则方程x2+ax+a-2=0的两个根为x1,x2,得x1+x2=-a,x1x2=a-2,
∴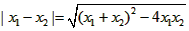 =
=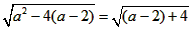 ,
,
当a=2时,两点间的距离最小。
