问题
解答题
已知两实数x,y满足
求:(1)z=3x-2y的最大值; (2)z=x2+y2-10y+25的最小值. |
答案
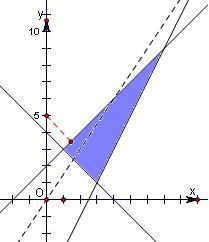
(1)由约束条件x-y+2≥0 x+y-4≥0 2x-y-5≤0
表示的可行域如图,
直线2x-y-5=0与直线 x+y-4=0的交点(3,1)作直线3x-2y=0的平行线l,
当l经过(3,1)时,z取得最大值,3×3-2×1=7.
(2)由于z=x2+y2-10y+25=x2+(y-5)2,
z=x2+y2-10y+25的几何意义是点P(x,y)到点(0,5)的距离的平方,
所以z=x2+y2-10y+25的最小值为:原点到直线x-y+2=0的距离的平方:
d2=(
)2,|-5+2| 2
即z=x2+y2-10y+25的最小值zmin=
.9 2