设k=

y

x

，则k的几何意义为过原点的直线的斜率，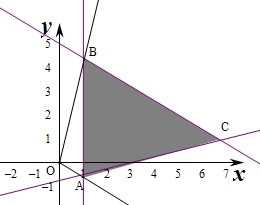

作出不等式组对应的平面区域如图（阴影部分ABC）：

则由图象可知，过原点的直线y=kx，当直线y=kx，经过点A时，直线的斜率k最小，

当经过点B时，直线的斜率k最大，

由

x=1 x-4y=3

，解得

x=1 y=- 1 2

，即A（1，-

1

2

），此时kOA=

- 1 2

1

=-

1

2

．

由

x=1 3x+5y=25

，解得

x=1 y= 22 5

，即B（1，

22

5

），此时k=

22

5

，

∴直线y=kx的斜率k的取值范围是-

1

2

≤k≤

22

5

，

故答案为：[-

1

2

，

22

5

]．