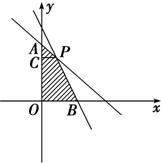
由约束条件作出其所确定的平面区域（阴影部分），其四个顶点为O（0，0），B（3，0），A（0，5），P（1，4）．

过P点作y轴的垂线，垂足为C．

则AC=|5-4|=1，PC=|1-0|=1，

OC=4，OB=3，AP=

2

，

PB=

(4-0)2+(1-3)2

=2

5

．

得S_△ACP=

1

2

AC•PC=

1

2

，

S_梯形COBP=

1

2

（CP+OB）•OC=8．

∴S=S_△ACP+S_梯形COBP=

17

2

．

平移直线z=4x+3y，由图象可知当直线z=4x+3y经过点P（1，4），

目标函数z=4x+3y取得最大值，最大值为16．