问题
解答题
已知A(3,
(1)求
(2)求z=
|
答案
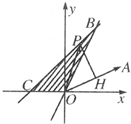
(1)作出可行域如图,则
=|
•OA OP |
|OA
|cos∠AOP,OP
又∠AOP是
与OA
的夹角,OP
∴目标函数
表示
•OA OP |
|OA
在OP
上的投影,OA
过P作
的垂线PH,垂足为H,OA
当P在可行域内移动到直线
x-y=0和直线x-3
y+2=0的交点B(1,3
)时,3
在OP
上的投影为|OA
|最大,此时|OH
|=|OP
|=2,∠AOP=∠AOB=OB
,π 6
∴
的最大值为|
•OA OP |
|OA
|cos∠AOB=2cosOB
=π 6 3
(2)z=
=|
•OA OP |
|OP
|cos∠AOP=2OA
cos∠AOP,3
因为∠AOP=[
,π 6
],所以当∠AOP=5π 6
时,zmax=2π 6
cos3
=3;π 6
当∠AOP=
时,zmin=25π 6
cos3
=-3.∴z=5π 6
的取值范围为[-3,3].
•OA OP |
|OP