问题
解答题
袋中有大小相同的4个红球与2个白球．
（1）若从袋中依次不放回取出一个球，求第三次取出白球的概率；
（2）若从袋中依次不放回取出一个球，求第一次取出红球的条件下第三次仍取出红球的概率．
（3）若从中有放回的依次取出一个球，记6次取球中取出红球的次数为ξ，求P（ξ≤4）与E（9ξ﹣1）．
答案
解：（1）从袋中依次不放回取出一个球取三次共有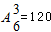
种情况，
第三次取出白球共有
种情况
∴从袋中依次不放回取出一个球，第三次取出白球的概率为
；
（2）第一次取出红球后，还剩下3红2白，共5个球，
故第一次取出红球的条件下第三次仍取出红球的概率为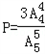
=
；
（3）记取一次球取出红球为事件A，则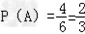
，
ξ服从二项分布，即ξ～B（6，
）
∴
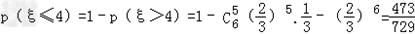
∵Eξ=6×
=4
∴E（9ξ﹣1）=9Eξ﹣1=9×4﹣1=35
