问题
解答题
盒中有大小形状相同的5只白球，2只黑球，用随机模拟法求下列事件的概率：
（1）任取1只球，得到白球；
（2）任取3只球，恰有2只白球；
（3）任取3只球（分三次每次放回再取），恰有3只白球。
答案
解：用1，2，3，4，5表示白球，6，7表示黑球，任取三球，即每三个数一组，每组中的数字不同；而任取三球（分三次每次放回再取），每组中的三个数字可以相同，于是，用计算器或计算机产生1到7之间的取整数值的随机数，
（1）统计随机数个数N及小于6的个数N1，则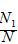
即为任取一球，得到白球的概率的近似值；
（2）三个一组（每组中数字不重复），统计总组数M及恰有两个数字小于5的组数M1，则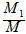
即为任取3球，恰有2只白球的概率的近似值；
（3）三个一组（每组中数字可以重复），统计总组数K及三个数字都小于6的组数K1，则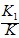
即为任取3球，恰有3只白球的概率的近似值。
