问题
解答题
从1、2、3、4、5、8、9这7个数中任取三个数,共有35种不同的取法(两种取法不同,指的是一种取法中至少有一个数与另一种取法中的三个数都不相同)。
(1)求取出的三个数能够组成等比数列的概率;
(2)求取出的三个数的乘积能被2整除的概率。
答案
解:(1)从1、2、3、4、5、8、9这7个数中任取三个数,每一种不同的取法为一个基本事件,
由题意可知共有35个基本事件,
设取出的三个数能组成等比数列为事件A,
事件A包含(1,2,4)、(2,4,8)、(1,3,9)共3个基本事件,
由于每个基本事件出现的可能性相等,
所以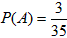 ;
;
(2)设取出的三个数的乘积能被2整除为事件B,
其对立事件为C,C包含(1,3,5)、(1,3,9)、(1,5,9)、(3,5,9)共4个基本事件,
由于每个基本事件出现的可能性相等,
所以P(C)=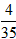 ,
,
所以P(B)=1-P(C)= 。
。
