（1）分别从集合P和Q中随机取一个数作为a和b，有（-1，-2）、（-1，1）、（-1，2）、

（2，-2）、（2，1）、（2，2）、（3，-2）、（3，1）和（3，2）共9个基本事件．

∵二次函数f（x）=ax²-4bx+1的图象的对称轴为x=

2b

a

，要使函数f（x）=ax²-4bx+1在区间

[1，+∞）上为增函数，当且仅当a＞0且

2b

a

≤1成立，即a＞0且2b≤a．

若a=2，则b=-2或1；若a=3，则b=-2或1．

由此可得满足条件的基本事件包含基本事件的个数是2+2=4．

∴函数y=f（x）在区间[1，+∞）上是增函数的概率为P=

4

9

；

（2）由（1）知当且仅当a＞0且2b≤a时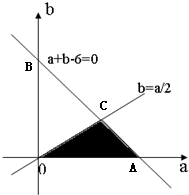，函数y=f（x）在区间[1，+∞）上是增函数．

根据题意全部结果所构成的区域为满足不等式

x+y-6≤0 x＞0 y＞0

的实数对（a，b）构成的集合，相应的区域为如右图的△OAB及其内部．

其中符合“函数f（x）在区间[1，+∞）上是增函数”的实数对（a，b），满足不等式

a+b-6＜0 a＞0且b＞0 2b≤a

，相应的区域为如右图的△OAC及其内部．

∵A（6，0），B（0，6），C（4，2），

∴S_△OAB=

1

2

×6×6=18，S_△OAC=

1

2

×6×2=6

∴所求事件的概率为P=

S△OAC

S△OAB

=

6

18

=

1

3

．