问题
解答题
设实数x,y满足不等式组
(1)作出点(x,y)所在的平面区域并求出x2+y2的取值范围; (2)设m>-1,在(1)所求的区域内,求Q=y-mx的最值. |
答案
(1)将不等式去绝对值,化简为:
或x+y≥1 x+y≤4 2x-y-5≤0 x≥ 3 2 x+y≥1 x+y≤4 2x+y-1≥0 x< 3 2
平面区域为如图所示的四边形DEFG及其内部,其中D(-3,7),E(0,1),F(2,-1),G(3,1);
由图可知,当动点(x,y)与点D(-3,7)重合时,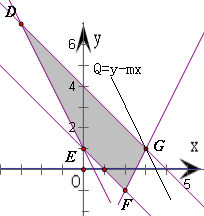
x2+y2达到最大值,最大值为OD2=9+49=58;
当动点(x,y)与原点在直线EF上的射影重合时,
x2+y2达到最小值,最小值为1 2
∴x2+y2的取值范围是[
,58]1 2
(2)作直线l:Q=y-mx,则它的斜率k=m(k>-1)
运动直线l,并观察图形可得:
①当-1<k≤2即-1<m≤2时
平移l到经过D点时,Q=y-mx值最大,Qmax=7+3m;
平移l到经过F点时,Q=y-mx值最小Qmin=-1-2m
②当k>2,即m>2时,
平移l到经过D点时,Q=y-mx值最大,Qmax=7+3m
平移l到经过G点时,Q=y-mx值最小Qmin=1-3m.
