问题
解答题
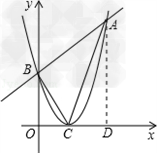
已知抛物线y=（x﹣2）2的顶点为C，直线y=2x+4与抛物线交于A、B两点，试求S△ABC．
答案
解：易知：抛物线y=（x﹣2）2的顶点C的坐标为（2，0），
联立两函数的解析式，得：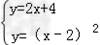
，
解得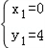
，
．
所以A（6，16），B（0，4）．
如图：过A作AD⊥x轴，垂足为D；
则S△ABC=S梯形ABOD﹣S△ACD﹣S△BOC
=
（OB+AD）·OD﹣
OC·OB﹣
CD·AD
=
（4+16）×6﹣
×2×4﹣
×4×16
=24．
