问题
填空题
某企业生产甲、乙两种产品,已知生产每吨甲产品要用3t原料A,2t天然气B;生产每吨乙产品要用1t原料A,3t天然气B,销售每吨甲产品可获得利润5万元,销售每吨乙产品可获得利润3万元.若该企业在一个生产周期内消耗的原料A不超过13t,B不超过18t,则该企业可获得最大利润为______万元.
答案
设生产甲产品x吨,生产乙产品y吨,
则有
,x>0 y>0 3x+y≤13 2x+3y≤18
该企业可获得利润z=5x+3y,
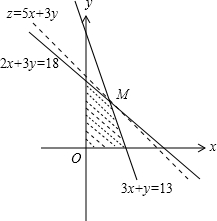
如图作出可行域,
由z=5x+3y,知y=-
x+5 3
,z 3
作出直线系y=-
x+5 3
,z 3
当直线经过可行域上的点M时,
纵截距达到最大,即z达到最大,
由
,解得:3x+y=13 2x+3y=18
,x=3 y=4
此时,zmax=5×3+3×4=27,
∴当甲产品生产3吨,乙产品生产4吨时,
企业获得最大利润,最大利润为27万元.