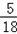问题
解答题
在平面直角坐标系xOy中,点P(x﹣2,x﹣y).
(1)在一个盒子中,放有标号为1,2,3的三张卡片,现从盒中有放回地先后随机抽取两张上卡片,它们的标号分别记为x,y,求事件“|OP|取到最大值”的概率;
(2)若在区间[0,3]上先后随机地取两个数分别记为经x,y,求点P在第一象限的概率.
答案
解:(1)记先后抽到的两张卡片的标号为(x,y),则

由表格可知|OP|的最大值为 .
.
设事件A为“|OP|取到最大值”则P(A)=
(2)设事件B为“点P在第一象限”,则事件B所构成的区域为
B={(x,y)|0≤x≤3,0≤y≤3,x﹣2>0,x﹣y>0}
由题意可知,基本事件空间可表示为Ω={(x,y)|0≤x≤3,0≤y≤3}
而Ω={(x ,y )|0 ≤x ≤3 ,0 ≤y ≤3}所表示的区域面积为9
B={(x,y)|0≤x≤3,0≤y≤3,x﹣2>0,x﹣y>0}表示的区域如图所示的阴影部分其面积为
由几何概型可知P(B)=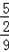 =
=