某工厂的一个车间生产某种产品,其成本为每公斤27元,售价为每公斤50元.在生产产品的同时,每公斤产品产生出0.3立方米的污水,污水有两种排放方式:
其一是输送到污水处理厂,经处理(假设污水处理率为85%)后排入河流;
其二是直接排入河流.
若污水处理厂每小时最大处理能力是0.9立方米污水,处理成本是每立方米污水5元;环保部门对排入河流的污水收费标准是每立方米污水17.6元,根据环保要求该车间每小时最多允许排入河流中的污水是0.225立方米.试问:该车间应选择怎样的生产与排污方案,才能使其净收益最大.
设车间每小时的净收益为z元,生产的产品为每小时x公斤,直接排入河流的污水量为每小时y立方米,则该车间每小时产生的污水量为0.3x,污水处理量0.3x-y,经污水处理后的污水排放量为(1-0.85)(0.3x-y),车间成本为27x,车间收入为50x,车间应交纳排污费用为17.6[(1-0.85)(0.3-y)+y],车间应交纳污水处理费5(0,3x-y),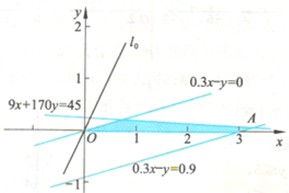
于是z=50x-27x-5(0.3x-y)-17.6[0.15(0.3x-y)+y]=20.708x-9.96y.
由题意得
,0.3x-y≤0.9 9x+170y≤45 0.3x-y≥0 x≥0,y≥0
作出可行域,由图中可以看出直线z=20.708x-9.96y在两条直线0.3x-y=0和9x-170y=45的交点处达到最大值,
其交点坐标为(3.3,0.09),此时zmax=67.44.
故该车间应每小时生产3.3公斤产品,直接排入河流的污水量为每小时0.09立方米,这样净收益最大.
