问题
解答题
一个口袋内装有形状、大小相同的2个白球和3个黑球.
(1)从中随机地摸出一个球不放回,再随机地摸出一个球,求两球同时是黑球的概率;
(2)从中随机地摸出 一个球,放回后再随机地摸出一个球,求两球颜色恰好不同的概率.
答案
解:设2个白球的编号为1、2,3个黑球的编号为3、4、5;x、y分别表示第一次、第二次取球的编号,则用数组(x,y)表示两次取球的结果.
所有的结果列表如下:
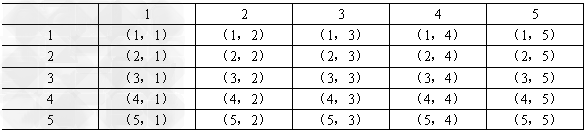
(1)设事件A为两球同时是黑球.
由表可知,无放回的抽取方法即两次的数字不相同的取法有20种,事件A包含6种,
所以P(A)=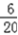 =
= 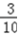 ;
;
(2)设事件B为摸出的两球恰好颜色不同.
由表可知,所以等可能的取法有25种,事件B包含12种,
所以P(B)=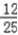 .
.
