问题
解答题
某人有楼房一幢，室内面积共180㎡,拟分隔两类房间作为旅游客房．大每间面积为18㎡，可住游客5名，每名游客每天住宿费为40元；小房间每间面积为15㎡，可住游客3名，每名游客每天住宿费为50元；装修大房间每间需1000元，装修小房间每间需600元．如果他只能筹款8000元用于装修，且游客能住满客房，他应隔出大房间和小房间各多少间，能获得最大收益？
答案
其一是将楼房室内全部隔出小房间１２间；其二是隔出大房间３间，小房间８间
消耗量 |
项目 |
 
| 装修费 （元） | 面积 （㎡） | 利润 （元） | |
| 大房间（间） | 1000 | 18 | 5×40 | |
| 小房间（间） | 600 | 15 | 3×50 | |
| 限额 | 8000 | 180 |  |
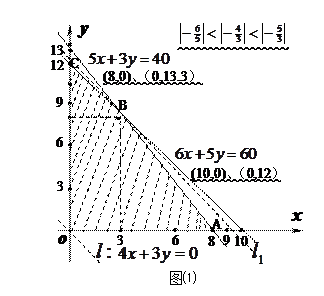设应隔出大、小房间分别为x,y间，此时收益为z元，则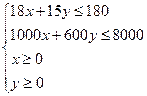
将上述不等式组化为
作出可行域，如图⑴，作直线l:200x+150y=0,即l:4x+3y=0.
将直线l向右平移，得到经过可行域的点B，且距原点最远的直线l1.
解方程组
得最优解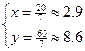 
但是房间的间数为整数，所以，应找到是整数的最优解．
① 当x=3时，代入5x+3y=40中，得
，得整点（3，8），此时z=200×3＋150×8=1800（元）;
② 当x=2时,代入6x+5y=60中，得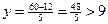
，得整点（2，9），此时z=200×2＋150×9=1750（元）；
③ 当x=1时,代入6x+5y=60中，得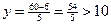
，得整点（1，10）,
此时z=200×1＋150×10=1700（元）；
④ 当x=0时,代入6x+5y=60中，得
，得整点（0，12），此时z=150×12=1800（元）．
由上①～④知，最优整数解为（0，12）和（3，8）．
答：有两套分隔房间的方案：其一是将楼房室内全部隔出小房间１２间；其二是隔出大房间３间，小房间８间，两套方案都能获得最大收益为１８００元．