某工厂生产甲、乙两种产品,计划每天每种产品的生产量不少于15吨,已知生产甲产品1吨,需煤9吨,电力4千瓦时,劳力3个;生产乙产品1吨,需煤4吨,电力5千瓦时,劳力10个;甲产品每吨的利润为7万元,乙产品每吨的利润为12万元;但每天用煤不超过300吨,电力不超过200千瓦时,劳力只有300个.问每天生产甲、乙两种产品各多少吨,才能使利润总额达到最大?
每天生产甲产品20吨、乙产品24吨,才能使利润总额达到最大
设每天生产甲、乙两种产品分别为x吨、y吨,利润总额为z万元, 1分
则线性约束条件为 , 4分
, 4分
目标函数为z=7x+12y, 8分
作出可行域如图,
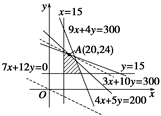
作出一组平行直线7x+12y=t,当直线经过直线4x+5y=200和直线3x+10y=300的交点A(20,24)时,
利润最大. 12分
即生产甲、乙两种产品分别为20吨、24吨时,利润总额最大,zmax=7×20+12×24=428(万元).
答 每天生产甲产品20吨、乙产品24吨,才能使利润总额达到最大. 14分
