问题
解答题
已知：关于x的方程ax2-(1-3a)x+2a-1=0．
(1)当a取何值时，二次函数y= ax2-(1-3a)x+2a-1的对称轴是直线x= -2；
(2)求证：a取任何实数时，方程ax2-(1-3a)x+2a-1=0总有实数根，
答案
解：(1) ∵二次函数y= ax2-(1-3a)x+2a-l的对称轴是x=-2，
∴
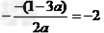解得a= -1，
经检验a= -1是原分式方程的解．
所以a=-1时，二次函数y= ax2-(1- 3a) x+2a -1的对称轴是直线x=-2；
(2)
①当a=0时，原方程变为-x- 1=0，
方程的解为x=-1;
②当a≠0时，原方程为一元二次方程ax2-(1- 3a)x+2a- 1=0，
当b2 -4ac≥0时，方程总有实数根，
∴[-(1-3a)] 2 -4a(2a-1)≥0, 整理得，a2- 2a+1≥0．即(a-1) 2>0．
∵a≠0时，（a-1）2≥0总成立，
所以a取任何实数时，方程ax2-(1- 3a)x+2a- 1=0 总有实数根．