问题
解答题
| 已知三个正数a,b,c满足a<b<c. (1)若a,b,c是从{
(2)若a,b,c是从(0,1)中任取的三个数,求a,b,c能构成三角形三边长的概率. |
答案
(1)若a,b,c能构成三角形,则a+b>c,c≥
.4 10
①若c=
时,b=4 10
,a=3 10
.共1种;2 10
②若c=
时.b=5 10
,a=4 10
,3 10
.共2种;2 10
同理c=
时,有3+1=4种;c=6 10
时,有4+2=6种;c=7 10
时,有5+3+1=9种;c=8 10
时,有6+4+2=12种.9 10
于是共有1+2+4+6+9+12=34种.
下面求从{
,1 10
,…2 10
}中任取的三个数a,b,c(a<b<c)的种数:9 10
①若a=
,b=1 10
,则c=2 10
,…,3 10
,有7种;b=9 10
,c=3 10
,…,4 10
,有6种;b=9 10
,c=4 10
,…,5 10
,有5种;…; b=9 10
,c=8 10
,有1种.9 10
故共有7+6+5+4+3+2+1=28种.
同理,a=
时,有6+5+4+3+2+1=21种;a=2 10
时,有5+4+3+2+1=15种;a=3 10
时,有4+3+2+1=10种;a=4 10
时,有3+2+1=6种;a=5 10
时,有2+1=3种;a=6 10
时,有1种.这时共有28+21+15+10+6+3+1=84种.7 10
∴a,b,c能构成三角形的概率为
=34 84
.17 42
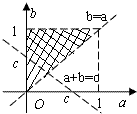
(2)a,b,c能构成三角形的充要条件是
.0<a<b<c<1 a+b>c 0<c<1
在坐标系aOb内画出满足以上条件的区域(如右图阴影部分),
由几何概型的计算方法可知,只求阴影部分的面积与图中正方形的面积比即可.
又S阴影=
,于是所要求的概率为P=1 2
=1 2 1
.1 2
