问题
解答题
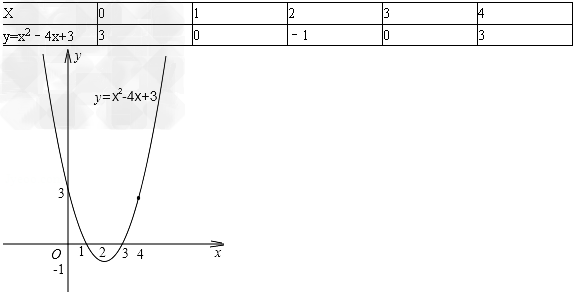
对于抛物线y=x2﹣4x+3,
(1)与y轴的交点坐标是 _______ ,与x轴交点坐标是 ______ ,顶点坐标是 _________ ;
(2)利用描点法画出函数的图象.
答案
解:(1)当x=0时,y=3,则与y轴的交点坐标为(0,3);
当y=0时,x2﹣4x+3=0,
解得,(x﹣1)(x﹣3)=0,
x1=1,x2=3,则与x轴的交点坐标为(1,0),(3,0);
原式可化为y=x2﹣4x+4﹣1=(x﹣2)2﹣1,
其顶点坐标为(2,﹣1).
(2)列表