问题
解答题
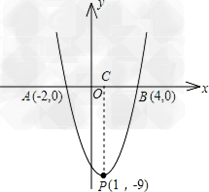
已知抛物线y=x2﹣2x﹣8．
（1）试说明该抛物线与x轴一定有两个交点．
（2）若该抛物线与x轴的两个交点分别为A、B（A在B的左边），且它的顶点为P，求△ABP的面积．
答案
解：（1）解方程x2﹣2x﹣8=0，得x1=﹣2，x2=4．故抛物线y=x2﹣2x﹣8与x轴有两个交点．
（2）由（1）得A（﹣2，0），B（4，0），故AB=6．
由y=x2﹣2x﹣8=x2﹣2x+1﹣9=（x﹣1）2﹣9，
故P点坐标为（1，﹣9）；
过P作PC⊥x轴于C，则PC=9，
∴S△ABP=
AB×PC=
×6×9=27．
