问题
证明题
求证ab+bc+cd+da≤a2+b2+c2+d2并说出等号成立的条件。
答案
证明：ab+bc+cd+da-（a2+b2+c2+d2）
=-
[2a2+2b2+2c2+2d2-2ab-2bc-2cd-2da]
=
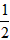[（a-b）2+（b-c）2+（c-d）2+（d-a）2]≥0，
当且仅当a=b=c=d时，等号成立。
搜题请搜索小程序“爱下问搜题”
求证ab+bc+cd+da≤a2+b2+c2+d2并说出等号成立的条件。
证明：ab+bc+cd+da-（a2+b2+c2+d2）
=-[2a2+2b2+2c2+2d2-2ab-2bc-2cd-2da]
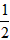=[（a-b）2+（b-c）2+（c-d）2+（d-a）2]≥0，
当且仅当a=b=c=d时，等号成立。