问题
解答题
已知函数y=f(x)的反函数。定义:若对给定的实数a(a≠0),函数y=f(x+a)与y=f-1(x+a)互为反函数,则称y=f(x)满足“a和性质”;若函数y=f(ax)与y=f-1(ax)互为反函数,则称y=f(x)满足“a积性质”。
(1)判断函数g(x)=x2+1(x>0)是否满足“1和性质”,并说明理由;
(2)求所有满足“2和性质”的一次函数;
(3)设函数y=f(x)(x>0)对任何a>0,满足“a积性质”。求y=f(x)的表达式。
答案
解:(1)函数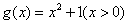 的反函数是
的反函数是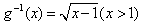 ,
,
∴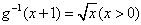 ,
,
而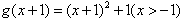 ,其反函数为
,其反函数为 ,
,
故函数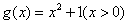 不满足“1和性质”;
不满足“1和性质”;
(2)设函数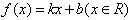 满足“2和性质”,k≠0,
满足“2和性质”,k≠0,
∴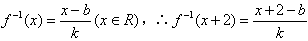 ,
,
而 ,
,
由“2和性质”定义可知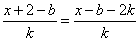 对x∈R恒成立,
对x∈R恒成立,
∴k=-1,b∈R,即所求一次函数为f(x)=-x+b(b∈R)。
(3)设a>0,x0>0,且点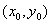 在y=f(ax)图像上,
在y=f(ax)图像上,
则 在函数
在函数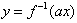 图象上,
图象上,
故 ,可得
,可得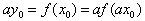 ,
,
令 ,
,
∴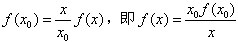 ;
;
综上所述, ,
,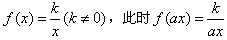 ,
,
其反函数就是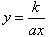 ,
,
而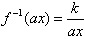 ,
,
故y=f(ax)与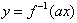 互为反函数。
互为反函数。
