问题
解答题
将三个小球随机地投入编号1,2,3,4的4个盒子中(每个盒子容纳的小球的个数没有限制),求:
(1)第1个盒子为空盒的概率;
(2)小球最多的盒子中小球的个数X的分布列和期望.
答案
(1)任意投放共有43=64(种)方法,若第1个盒子为空盒,则小球可随机地投入编号2,3,4的3个盒子中,有33=27(种)方法,故所求的概率为
.27 64
(2)小球最多的盒子中小球的个数X的取值为1,2,3.则
P(X=1)=
=A 34 43
;P(X=2)=3 8
=C 24
AC 23 22 43
;P(X=3)=9 16
=C 14 43
.1 16
故X的分布列为
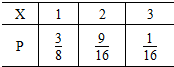
所以X的数学期望为E(X)=1×
+2×3 8
+3×9 16
=1 16
.27 16

 井字复合箍,
井字复合箍,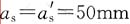 ;柱净高2800mm,弯矩反弯点位于柱高中部,试问,该柱的轴压比限值[μN],与下列何项数值最为接近()
;柱净高2800mm,弯矩反弯点位于柱高中部,试问,该柱的轴压比限值[μN],与下列何项数值最为接近()