问题
计算题
如图所示，四分之一圆轨道OA与水平轨道AB相切，它们与另一水平轨道CD在同一竖直面内，C点在B点的正下方，C、D两点间的距离为X＝8m；圆轨道OA的半径R＝0．2 m，OA与AB均光滑，一质量m＝1 kg的滑块从O点由静止释放，当滑块经过B点时，一小车由D点以初速度v0 ＝3m/s向C点做匀减速运动直到静止，加速度大小a＝1 m/s2，运动一段时间后滑块恰好落入小车中．（取g＝10 m/s2）求：
（1）滑块滑经A点时的速度大小；
（2）滑块到达A点时对轨道的压力大小；
（3）B、C两点间的高度h.
答案
（1）v=2m/s（2）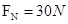
（3）h=20m
题目分析：（1）对滑块从O到A由动能定理得：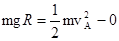
①
解得：v=2m/s ②
（2）在A点有：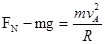
③
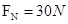解得： ④
由牛顿第三定律得滑块对轨道的压力大小为30N ⑤
（3）由题意得：X=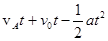
⑥
解得：t=2s ⑦
由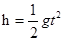
⑧
解得：h=20m ⑨
点评：本题是圆周运动与平抛运动、匀减速直线运动的综合，是常见的题型．关键是分析各个运动过程之间的关系．