问题
问答题
已知某股票当前的股价为62元，看涨期权执行价格为70元，距离到期口的时间为4周，股价的方差为0.35，无风险年利率为5%，假设该期权为欧式期权。
要求：
（1）利用布莱克—斯科尔斯期权定价模型为该看涨期权定价。
（2）在套利驱动的均衡状态下，确定与该看涨期权具有相同执行价格和到期日的看跌期权的价格。
答案
参考答案：
(1)①
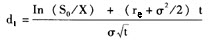
=(-0.1214+0.0173)/0.1641
=-0.6344
②d2=d1-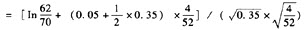
=-0.6344-
=-0.7985
③通过N(0.63)=0.7357和N(0.64)=0.7389之间插值来计算N(0.6344)：
N(0.6344)=0.7357+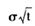
×(0.7389-0.7357)=0.7371
N(-0.6344)=1-N(0.6344)=1-0.7371=0.2629
通过N(0.79)=0.7852和N(0.80)=0.7881之间插值来计算N(0.7985)：
N(0.7985)=0.7852+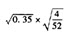
×(0.7881-0.7852)=0.7877
N(-0.7985)=1-N(0.7985)=1-0.7877=0.2123
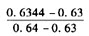
=62×0.2629-70×e-0.05×(4/52)×0.2123
=62×0.2629-69.73×0.2123
=16.30-14.80
=1.5(元)。
(2)在套利驱动的均衡状态下，看跌期权的价格=看涨期权价格+执行价格的现值-标的资产现行价格
=1.5+70×e-0.05×(4/52)-62=1.5+69.73-62=9.23 (元)
或者为了简化起见，执行价格的现值=70/(1+0.05×4/52)=69.74(元)，则看跌期权价值=看涨期权价格+执行价格的现值-标的资产现行价格
=1.5+69.74-62=9.24(元)。