问题
填空题
若x2+y2=4，则x-y的最大值是______．
答案
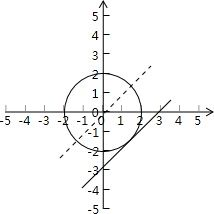
令b=x-y，则b是直线y=x-b在y轴上的截距的相反数，
∵该直线与圆x2+y2=4有公共点，
∴当直线与圆相切于第四象限时，截距取到最小值，
∵
=2，|b| 2
∴b=2
或b=-22
（舍去），2
∴b的最大值为2
．2
故答案为2
．2
搜题请搜索小程序“爱下问搜题”
若x2+y2=4，则x-y的最大值是______．
令b=x-y，则b是直线y=x-b在y轴上的截距的相反数，
∵该直线与圆x2+y2=4有公共点，
∴当直线与圆相切于第四象限时，截距取到最小值，
∵
=2，|b| 2
∴b=2
或b=-22
（舍去），2
∴b的最大值为2
．2
故答案为2
．2