问题
解答题
| 市环保局举办2013年“六•五”世界环境日宣传活动,进行现场抽奖.抽奖规则是:盒中装有10张大小相同的精美卡片,卡片上分别印有“环保会徽”或“绿色环保标志”图案.参加者每次从盒中抽取卡片两张,若抽到两张都是“绿色环保标志”卡即可获奖. (1)活动开始后,一位参加者问:盒中有几张“绿色环保标志”卡?主持人笑说:我只知道若从盒中抽两张都不是“绿色环保标志”卡的概率是
(2)现有甲乙丙丁四人依次抽奖,抽后放回,另一人再抽.用ξ表示获奖的人数.求ξ的分布列及E(ξ),D(ξ). |
答案
(1)从盒中任抽两张都不是“绿色环保标志”卡的概率是一个古典概型,
试验发生包含的事件数是C102,设环保会徽卡有n张,则有
=C 2n C 210
,得n=6,所以绿色环保标志”卡有4张,1 3
抽奖者获奖的概率为
=C 24 C 210 2 15
(2)ξ可能取的值为0,1,2,3,4,变量ξ服从二项分布,ɛ~B(
,4),根据二项分布的概率公式得到2 15
ξ的分布列为P(ξ=k)=
(C k4
)k(2 15
)4-k13 15
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||||||||||||||
| P | (
|
|
|
| (
|
| 2 |
| 15 |
| 8 |
| 15 |
| 2 |
| 15 |
| 2 |
| 15 |
| 104 |
| 225 |

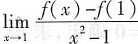 =().
=().