问题
计算题
如图所示，长为l的长木板A放在动摩擦因数为μ1的水平地面上，一滑块B（大小可不计）从A的左侧以初速度v0向右滑上木板，滑块与木板间的动摩擦因数为μ2（A与水平地面间的最大静摩擦力与滑动摩擦力大小相同）．已知A的质量为M=2.0kg，B的质量为m=3.0kg，A的长度为l=3.0m，v0="5m/s" ，μ1=0.2，μ2=0.4，（g取10m/s2 ）
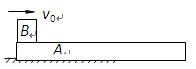
（1）A、B刚开始运动时各自的加速度分别是多大？
（2）为保证B在滑动过程中不滑出A，初速度v0应满足什么条件？
（3）分别求A、B对地的最大位移．
答案
（1）
、
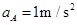（2）
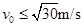
（3）A发生的位移0.75m、B发生的位移3.25m
题目分析：（1）分别对A、B受力分析，
根据牛顿第二定律：B物体的加速度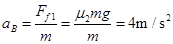 
A物体的加速度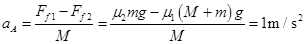
（2）设经过时间t，AB的速度相等则有：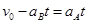
此时B刚好到达A的最右端
所以B发生的位移：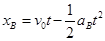 
A发生的位移：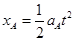
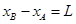
联立解得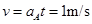
为保证B在滑动过程中不滑出A，则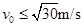
（3）设经过时间t，AB的速度相等则有：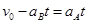
解得t=1s
A发生的位移：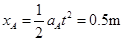
所以B发生的位移：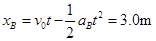
AB速度达到相等后，共同速度为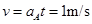
AB速度达到相等后，相对静止一起以v=1m/s的初速度，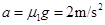
的加速度一起匀减速运动直到静止，发生的位移：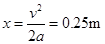 
所以A发生的位移为
B发生的位移为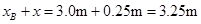
点评：本题属于多过程问题，在分析时要逐段、分物体求解，最好画出运动过程图。第（2）中要找到保证B在滑动过程中不滑出A时的临界条件。
