设f（x）=

-x2+2x+3

-

3

，根据二次函数的单调性，可得

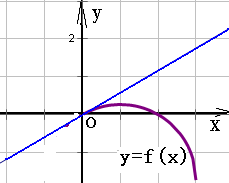
函数在[0，1]上为增函数，在[1，2]上为减函数．

设函数在 x=0 处，切线斜率为k，则k=f'（0）

∵f'（x）=

1

2

•

(-x2 +2x)′

-x2+2x+3

=

-x  +1

-x2+2x+3

，

∴k=f'（0）=

3

3

=tan30°，可得切线的倾斜角为 30°，

因此，要使旋转后的图象仍为一个函数的图象，

旋转θ后的切线倾斜角最多为 90°，

也就是说，最大旋转角为 90°-30°=60°，即θ的最大值为60°

故答案为：60°