问题
选择题
设x,y满足约束条件
|
答案
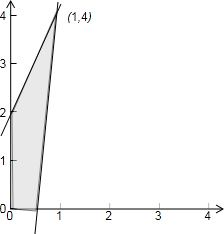
满足约束条件
的区域是一个四边形,2x-y+2≥0 8x-y-4≤0 x≥0 y≥0
如图,4个顶点是(0,0),(0,2),(
,0),(1,4),1 2
由图易得目标函数在(1,4)取最大值2,即
+1 a
=2,4 b
∴a+b=
(a+b)(1 2
+1 a
)=4 b
(5+1 2
+b a
)4a b
∵a>0,b>0,∴
+b a
≥24a b
=4
•b a 4a b
当且仅当
=b a
时,4a b
+b a
的最小值问44a b
∴a+b的最小值为9 2
故选A.
