问题
解答题
设函数f(x)=|x2﹣2x|.
(1)在区间[﹣2,6]上画出函数f(x)的图象;
(2)根据图象写出该函数在[﹣2,6]上的单调区间;
(3)方程f(x)=a有两个不同的实数根,求a的取值范围.(只写答案即可)
答案
解:(1)函数f(x)=|x2﹣2x|=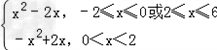
在区间[﹣2,6]上函数f(x)的图象如图:
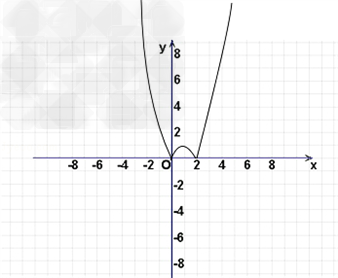
(2)根据图象可知,函数的单调增区间为[0,1]∪[2,+∞);
函数的单调减区间为(﹣∞,0]∪[1,2]
(3)考查两个函数y1=f(x)与y2=a,由图象可知当a=0或a≥1时方程有两个实数根.
