f（x）=x²-4x-4=（x-2）²-8，即抛物线开口向上，对称轴为x=2，最小值为-8，过点（0，-4），

结合二次函数的图象可知：

当t+1＜2，即t＜1时，f（x）=x²-4x-4，x∈[t，t+1]（t∈R）在x=t+1处取最小值f（t+1）=t²-2t-7，

当

t+1≥2 t≤2

，即1≤t≤2时，f（x）=x²-4x-4，x∈[t，t+1]（t∈R）在x=2处取最小值-8，

当t＞2时，f（x）=x²-4x-4，x∈[t，t+1]（t∈R）在x=t处取最小值f（t）=t²-4t-4，

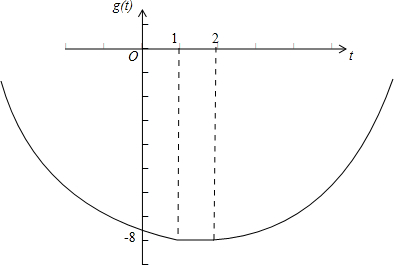
即最小值为g（t），由以上分析可得，g(t)=

t2-2t-7，t∈(-∞，1) -8，t∈[1，2] t2-4t-4，t∈(2，+∞)

，作图象如下；