问题
问答题
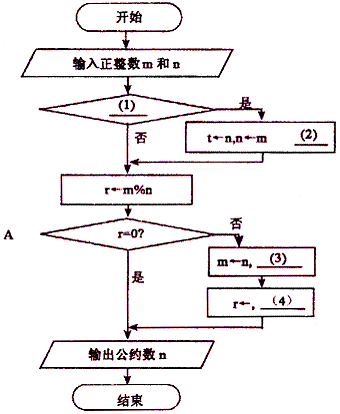
[说明] 下面的流程图采用欧几里得算法，实现了计算两正整数最大公约数的功能。给定正整数m和 n，假定m大于等于n，算法的主要步骤为： (1)以n除m并令r为所得的余数； (2)若r等于0，算法结束；n即为所求； (3)将n和r分别赋给m和n，返回步骤(1)。[流程图]
[问题1] 将流程图中的(1)～(4)处补充完整。[问题2] 若输入的m和n分别为27和21，则A中循环体被执行的次数是 (5) 。
答案
参考答案：
解析：[问题1] (1) n＞m或n≥m或其它等效形式
(2) m←t (3) n←r (4) m%n
[问题2] (5) 1
(1)～(2)当n的值大于(等于)m时，应交换两者的值，再使用欧几里得算法；
(3)～(4)略；
(5)m，n和r在执行循环A前后的值分别为：
| 变量取值 | m | n | r=m%n | 是否继续 |
| 执行循环A之前 | 27 | 21 | 6 | 是 |
| 执行一次循环A之前 | 21 | 6 | 3 | 是 |
| 执行两次循环A之后 | 6 | 3 | 0 | 否 |