问题
填空题
在不等式组
|
答案
由
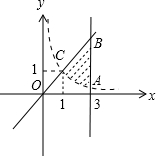
,得到可行域如图中阴影部分,y≤x 0<x≤3 y> 1 x
则阴影部分中的格点有(2,1),(2,2),(3,1),(3,2),(3,3)共5个点,
从中任取3个点,所有的取法种数为
=10种,C 35
其中只有1种情况共线,即取(3,1),(3,2),(3,3)三点时共线,不能构成三角形,
则3点恰能成为一个三角形的三个顶点的概率为p=
.9 10
故答案为
.9 10
在不等式组
|
由
,得到可行域如图中阴影部分,y≤x 0<x≤3 y> 1 x
则阴影部分中的格点有(2,1),(2,2),(3,1),(3,2),(3,3)共5个点,
从中任取3个点,所有的取法种数为
=10种,C 35
其中只有1种情况共线,即取(3,1),(3,2),(3,3)三点时共线,不能构成三角形,
则3点恰能成为一个三角形的三个顶点的概率为p=
.9 10
故答案为
.9 10
