问题
解答题
若函数f(x)=log3(ax2-x+a)有零点,求a的取值范围.
答案
解:∵f(x)=log3(ax2-x+a)有零点,
∴log3(ax2-x+a)=0有解,
∴ax2-x+a=1有解,
当a=0时,x=-1;
当a≠0时,若ax2-x+a-1=0有解,则Δ=1-4a(a-1)≥0,即4a2-4a-1≤0,
解得: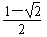 ≤a≤
≤a≤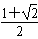 ,且a≠0;
,且a≠0;
综上所述,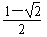 ≤a≤
≤a≤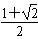 。
。
若函数f(x)=log3(ax2-x+a)有零点,求a的取值范围.
解:∵f(x)=log3(ax2-x+a)有零点,
∴log3(ax2-x+a)=0有解,
∴ax2-x+a=1有解,
当a=0时,x=-1;
当a≠0时,若ax2-x+a-1=0有解,则Δ=1-4a(a-1)≥0,即4a2-4a-1≤0,
解得: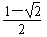 ≤a≤
≤a≤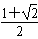 ,且a≠0;
,且a≠0;
综上所述,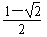 ≤a≤
≤a≤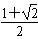 。
。