问题
计算题
如图所示，物体质量m1="0.1kg" ，视为质点，在C处弹簧发射器的作用下，沿光滑半圆轨道至最高点A处后在空中飞行，不计空气阻力，恰好沿PQ方向击中P点，∠PQC=530，半圆的半径R=0.5m，A、P两点的竖直距离为0.8米，g=10m/s2 ,sin530=0.8,cos530="0.6"
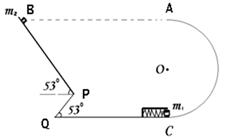
（1）此物体离开A点后作什么运动？在A点速度多大？A、P两点的水平距离为多大？物体在A点对轨道的压力有多大？
（2）质量m2=0.2kg的另一物体，也视为质点，放于与A点等高的光滑斜面BP上，其倾角为530，问：当质量m1的物体刚要离开轨道A点时，静止释放质量m2的物体应该提前还是滞后多少时间，才能实现两物体同时到达P点？
答案
（1）平抛运动，3m/s, 1.2m, 0.8N（2）提前0.1s
题目分析：（1）物体在A点时速度水平，只受重力，做平抛运动。
落到P点时，速度与水平方向夹角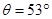
，A、P两点的竖直距离为h=0.8米，
由
得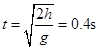
，
竖直分速度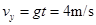
，
由于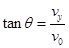
，
所以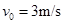
.
A、P两点的水平距离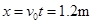
物体在A点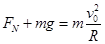
解得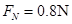
。
（2）斜面长度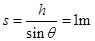
由牛顿第二定律可得mgsinθ=ma，解得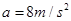
由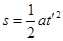
得物块下滑时间
，
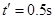所以物块下滑时间长，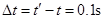
因此要想实现两物体同时到达P点，
应该提前0.1s
点评：本题的解题关键是质点恰好沿PQ方向击中P点，这句话的意思中确定了此时速度的方向与水平方向夹角为53º，根据此关系可以由竖直速度求出水平速度。