问题
解答题
设函数f(x)=|x2-2x|.
(1)画出f(x)=|x2-2x|在区间[-1,4]上函数f(x)的图象;并根据图象写出该函数在[-1,4]上的单调区间;
(2)试讨论方程f(x)=a在区间[-1,4]上实数根的情况,并加以简要说明.
答案
(1)f(x)=|x2-2x|=
.x2-2x,(-1≤x≤0或2≤x≤4) -x2+2x,(0<x<2)
图象如图:
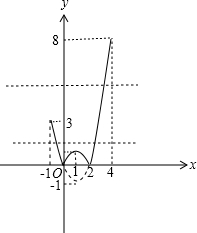
函数的减区间为[-1,0),[1,2);
函数的增区间为[0,1),[2,4].
(2)方程f(x)=a在区间[-1,4]上实数根,
即函数y=f(x)的图象与函数y=a的图象在区间[-1,4]上交点的横坐标.
由图象看出:a<0或a>8时,方程无实数根;
3<a≤8时,方程有一个实数根;
a=0或1<a≤3时,方程有两个实数根;
a=1时,有三个实数根;
0<a<1时,方程有四个实数根.
