问题
解答题
函数f(x)=|x-1||2-x|
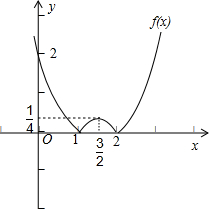
(1)作出函数f(x)的图象;
(2)方程f(x)=k(k∈R)中,k为何值时方程无解,2解,3解,4解?
答案
(1)函数f(x)=|x-1||2-x|=|(x-1)(x-2)|,如图所示:
(2)①若方程f(x)=k(k∈R)无解,则函数f(x)的图象和直线y=k没有交点,
数形结合可得 k<0,即当k<0时,方程f(x)=k(k∈R)无解.
②若方程f(x)=k(k∈R)有2个解,则函数f(x)的图象和直线y=k有2个交点,
数形结合可得 k>
,或k=0,即当k>1 4
,或k=0时,方程f(x)=k(k∈R)有2个解.1 4
③若方程f(x)=k(k∈R)有3个解,则函数f(x)的图象和直线y=k有3个交点,
数形结合可得 k=
,即当k=1 4
时,方程f(x)=k(k∈R)有3个解.1 4
若方程f(x)=k(k∈R)由4个解,则函数f(x)的图象和直线y=k有4个交点,
数形结合可得 0<k<
,即当 0<k<1 4
时,方程f(x)=k(k∈R)有4个解.1 4