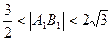问题
解答题
设f(x)=ax2+bx+c(a>b>c),f(1)=0,g(x)=ax+b.
(1)求证:函数y=f(x)与y=g(x)的图象有两个交点;
(2)设f(x)与g(x)的图象交点A、B在x轴上的射影为A1、B1,求|A1B1|的取值范围;
答案
(1)同解析,(2)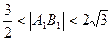
(1)由题意得: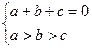 所以
所以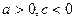
化简方程: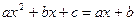 得:
得: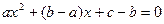
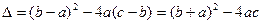
因为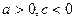 所以
所以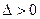
所以:函数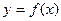 与
与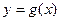 的图象有两个不同的交点
的图象有两个不同的交点
(2)设方程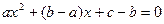 的两根为
的两根为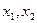 ,
,
则: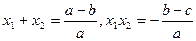
所以: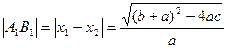 由于
由于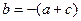
所以:
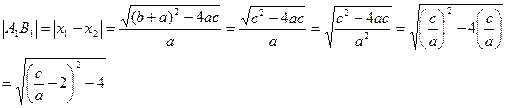
将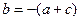 代入
代入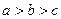 得:
得: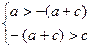 解得:
解得: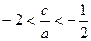
所以: