问题
填空题
已知函数f(x)＝|2x－1|，a<b<c，且f(a)>f(c)>f(b)，则下列结论中，一定成立的是________．
①a<0，b<0，c<0; ②a<0，b≥0，c>0；③2－a<2c; ④2a＋2c<2.
答案
④
由图示可知a<0时，b的符号不确定，1>c>0，故①②错；
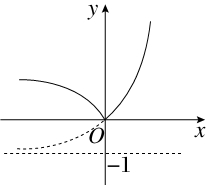
∵f(a)＝|2a－1|，f(c)＝|2c－1|，
∴|2a－1|>|2c－1|，
即1－2a>2c－1，
故2a＋2c<2，④成立．
又2a＋2c>2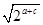
，∴2a＋c<1，
∴a＋c<0，∴－a>c，
∴2－a>2c，③不成立．