问题
计算题
粗糙绝缘的水平面附近存在一个平行于水平面的电场，其中某一区域的电场线与x轴平行，且沿x轴方向的电势φ与坐标值x的关系如下表格所示：
根据上述表格中的数据可作出如下的φ-x图像。现有一质量为0.10kg，电荷量为1.0×10-7C带正电荷的滑块（可视作质点），其与水平面的动摩擦因数为0.20。问：
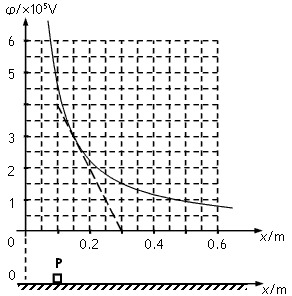
（1）由数据表格和图像给出的信息，写出沿x轴的电势φ与x的函数关系表达式。
（2）若将滑块无初速地放在x=0.10m处，则滑块最终停止在何处？
（3）在上述第（2）问的整个运动过程中，它的加速度如何变化？当它位于x=0.15m时它的加速度多大？
（4）若滑块从x=0.60m处以初速度v0沿-x方向运动，要使滑块恰能回到出发点，其初速度v0应为多大？
答案
解：（1）由数据表格和图像可得，电势φ与x成反比关系，即
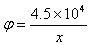V
（2）由动能定理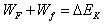
=0
设滑块停止的位置为x2，有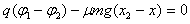
即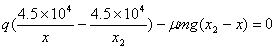
代入数据有1.0×10-7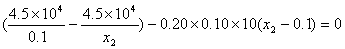
可解得x2=0.225m（舍去x2=0.1m）
（3）先做加速度减小的变加速运动，后做加速度增大的变减速运动，即加速度先减小后增大
当它位于x=0.15m时，图像上该点的切线斜率表示场强大小
E=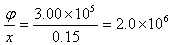
N/C
滑块在该点的水平合力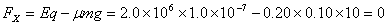
故滑块的加速度a=Fx/m =0
（4）设滑块到达的最左侧位置为x1，则滑块由该位置返回到出发点的过程中
由动能定理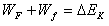
=0
有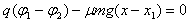
代入数据有1.0×10-7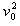
可解得x1=0.0375m（舍去x1=0.6m）
再对滑块从开始运动到返回出发点的整个过程，由动能定理
-2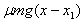
=
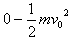
代入数据有2×0.20×0.10×10（0.60－0.0375）=0.5×0.10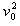
可解得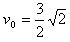
≈2.12m/s
