问题
解答题
已知函数f(x)=x3+2x2-ax+1，
(Ⅰ)若函数f(x)在点(1，f(1))处的切线斜率为4，求实数a的值；
(Ⅱ)若函数g(x)=f′(x)在区间（-l，1）上存在零点，求实数a的取值范围。
答案
解：由题意得g(x)=f′(x)=3x2+4x-a，
(Ⅰ)f′(1)=3+4-a=4，∴a=3。
(Ⅱ)解法一：（1）当g（-1）=-a-1=0，a=-1时，g(x)=f′(x)的零点
；
（2）当g（-1）=7-a=0时，f′(x)的零点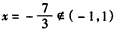
，不合题意；
（3）当g（1）g（-1）＜0时，-1＜a＜7；
（4）当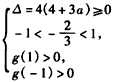
时，∴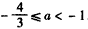
；
综上所述，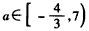
。
解法二：g(x)=f′(x)在区间（-1，1）上存在零点，等价于3x2+4x=a在区间（-1，1）上有解，
也等价于直线y=a与曲线y=3x2+4x，x∈（-1，1）有公共点，
作图可得。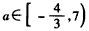
另解：又等价于当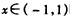
时，求值域，
。
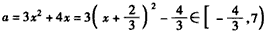