如图所示,小木块在沿斜面向上的恒定外力F作用下,从A点由静止开始作匀加速运动,前进了0.45m抵达B点时,立即撤去外力。此后小木块又前进0.15m到达C点,速度为零。已知木块与斜面动摩擦因数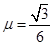 ,木块质量m=1kg。
,木块质量m=1kg。

求:(1)木块向上经过B点时速度为多大?
(2)木块在AB段所受的外力多大?( g="10" m/s2)
(1)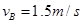 (2)F=10N
(2)F=10N
考点:牛顿第二定律;匀变速直线运动的速度与时间
题目分析:(1)对小滑块加速和减速过程分别受力分析,加速过程受推力、重力、支持力和摩擦力,减速过程,推力撤销,其余力不变;然后对两个过程运用牛顿第二定律求出加速度,再根据速度位移公式列式求解;
(2)依据第一问的解答,可以进一步得到外力F的大小;
(3)木块下降过程,先受力分析,受重力、支持力和摩擦力,根据牛顿第二定律求解加速度,再根据运动学公式求解木速度.
解:(1)撤去外力后,小木块做匀减速运动从B运动到C,
加速度大小为 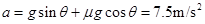
所以有 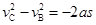
代入可解得 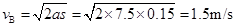
(2)设外加恒力为F则刚开始从A运动到B的加速度为
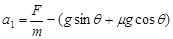
刚开始是做匀加速直线运动,故有: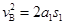
代入数据可求得: F=10N
点评:本题关键是对木块受力分析,根据牛顿第二定律求出各个时间段的加速度,然后根据运动学公式列式求解.

 Cu+H2O.下列有关H2、CO、C三种物质的说法正确的是 [ ]
Cu+H2O.下列有关H2、CO、C三种物质的说法正确的是 [ ]