问题
解答题
(12分)某班级有数学、自然科学、人文科学三个兴趣小组,各有三名成员,现从三个小组中各选出一人参加一个座谈会.
(I)求数学小组的甲同学没有被选中、自然小组的乙同学被选中的概率;
(II)求数学组的甲同学、自然小组的乙同学至少有一人不被选中的概率.
答案
 ,
,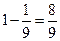
我们把数学小组的三位成员记作 ,自然小组的三位成员记作
,自然小组的三位成员记作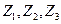 ,人文小组的三位成员记作
,人文小组的三位成员记作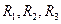 ,则基本事件是
,则基本事件是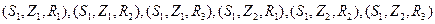 ,
,
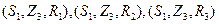 ,然后把这9个基本事件中
,然后把这9个基本事件中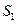 换成
换成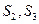 又各得
又各得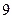 个基本事件,故基本事件的总数是
个基本事件,故基本事件的总数是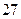 个.以
个.以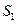 表示数学组中的甲同学、
表示数学组中的甲同学、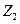 表示自然小组的乙同学.----------2分
表示自然小组的乙同学.----------2分
(I)甲同学没有选中、自然小组的乙同学被选中所含有的基本事件是上述基本事件中不含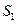 、含有
、含有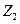 的基本事件,
的基本事件,
即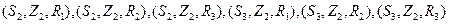 共6个基本事件,故所求的概率为
共6个基本事件,故所求的概率为 . ----------6分
. ----------6分
(II)“数学组的甲同学、自然小组的乙同学至少有一人不被选中”的对立事件是“数学组的甲同学、自然小组的乙同学都被选中”,这个事件所包含的基本事件是 ,共3个基本事件,这个事件的概率是
,共3个基本事件,这个事件的概率是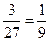 . ---------10分 根据对立事件的概率计算方法,所求的概率是
. ---------10分 根据对立事件的概率计算方法,所求的概率是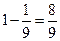 .----------12分
.----------12分
